Theoretical Physics: Statistical Mechanics
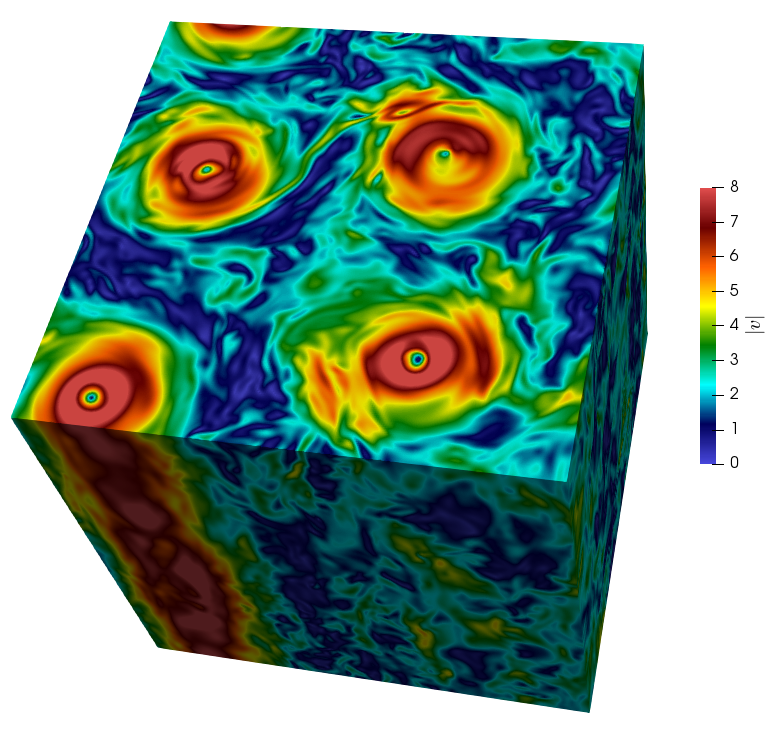
FIG1: Snapshot of velocity magnitude in a turbulent flow
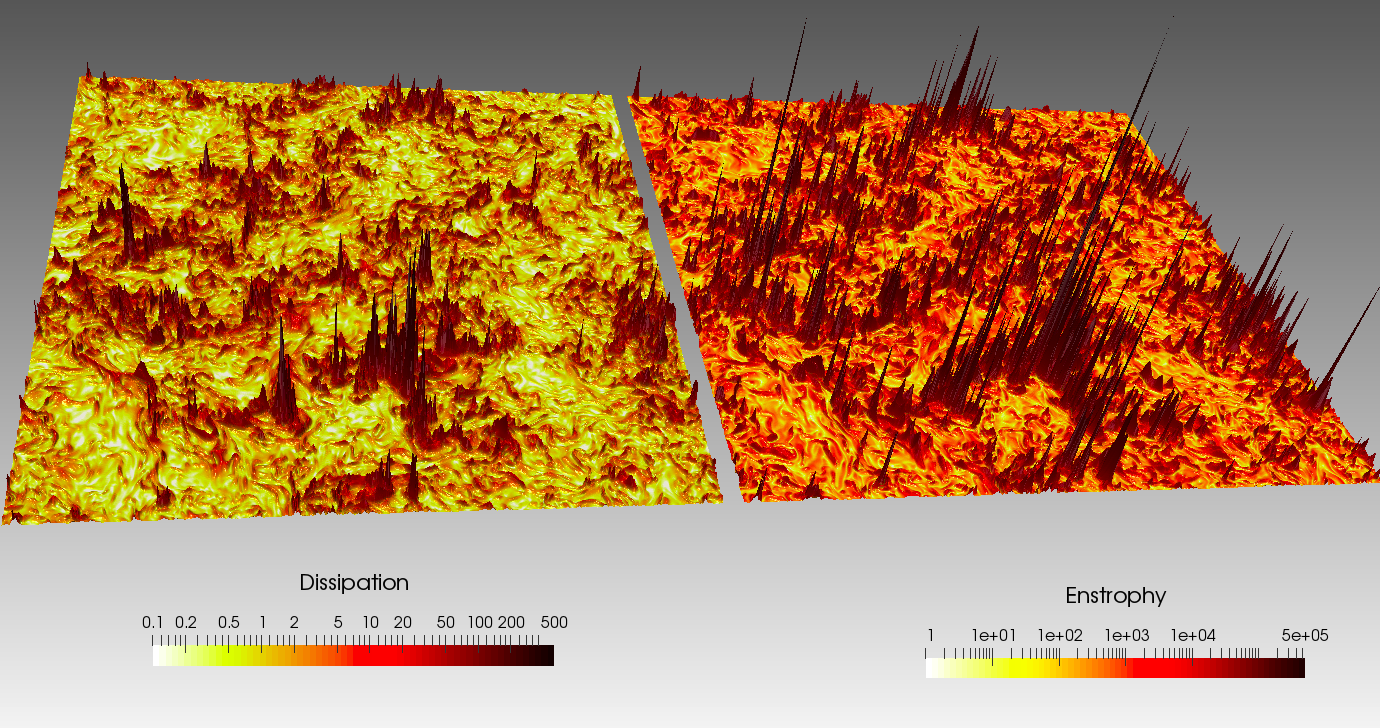
FIG2: Energy/Enstrophy dissipation in turbulent fluids

FIG3: Rheology of emulsions in structured microchannels
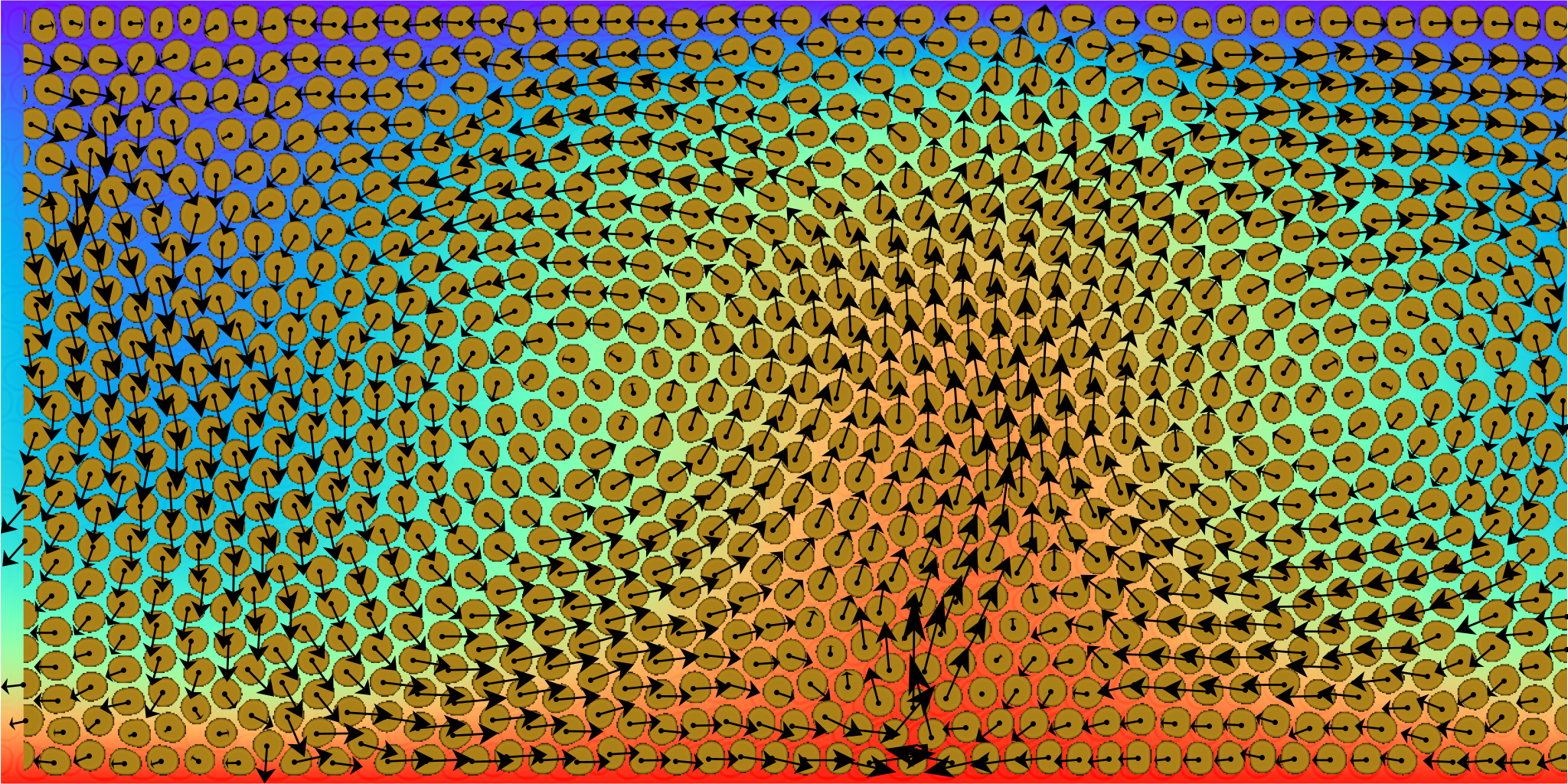
FIG4: Convection in multicomponent fluids

FIG5: Dynamics of viscoelastic membranes immersed in flow
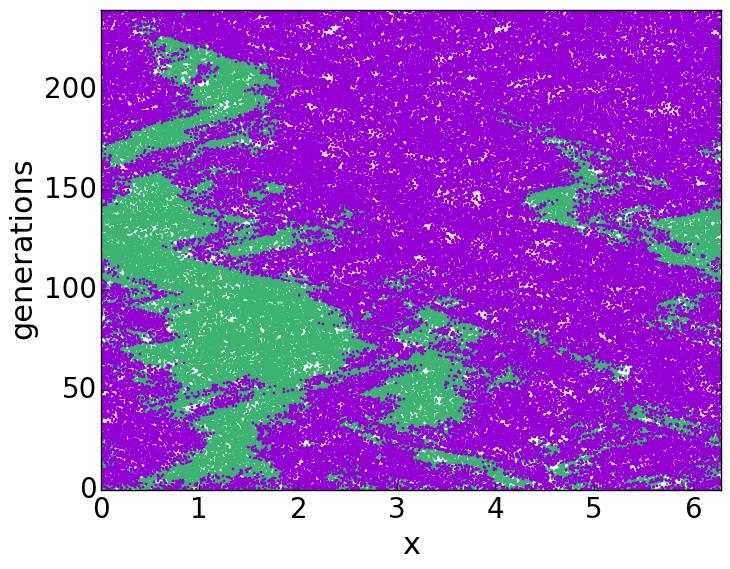
FIG6: Spatio-temporal evolution of micro-organisms
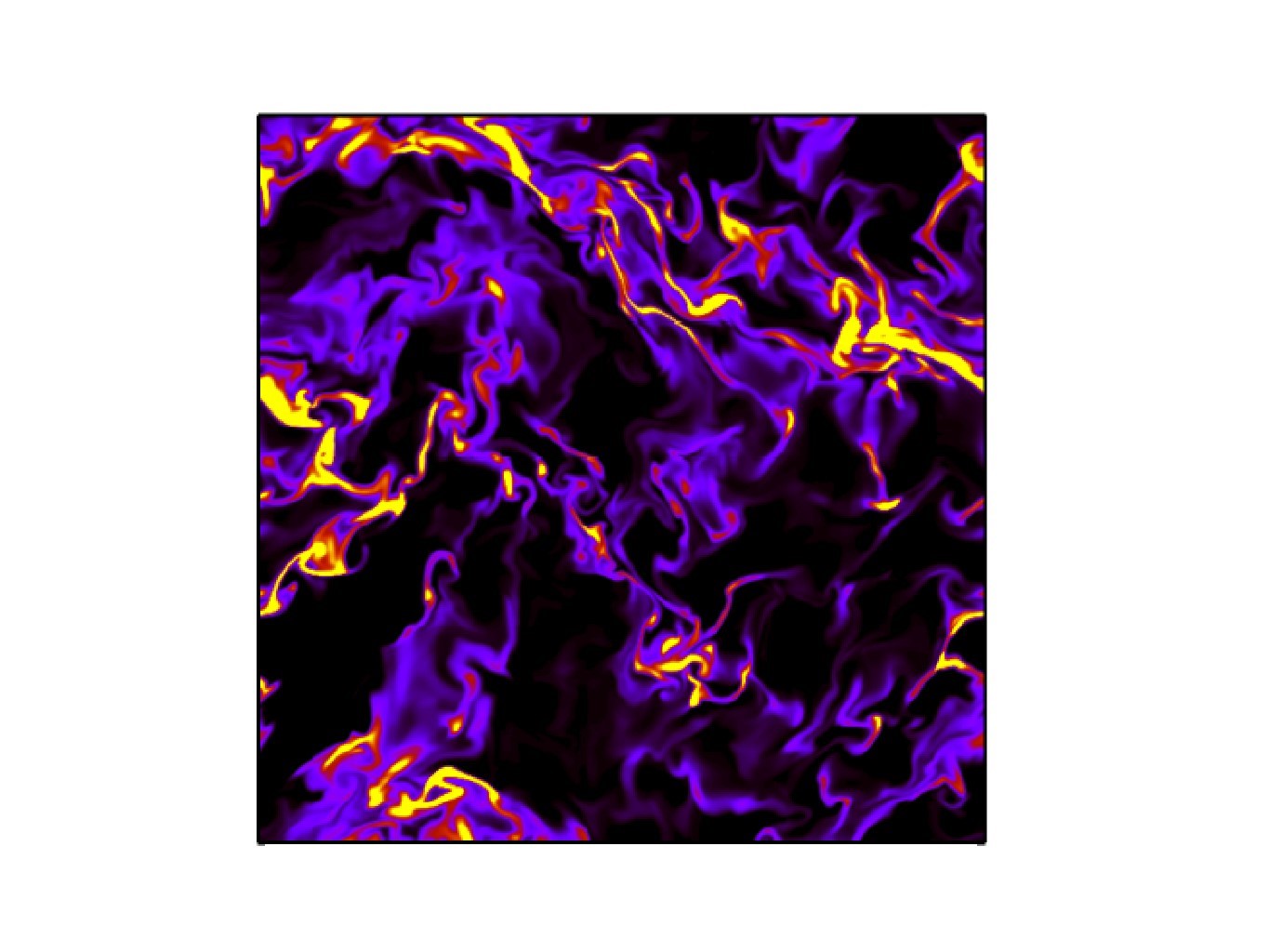
FIG7: Effects of turbulence on population dynamics
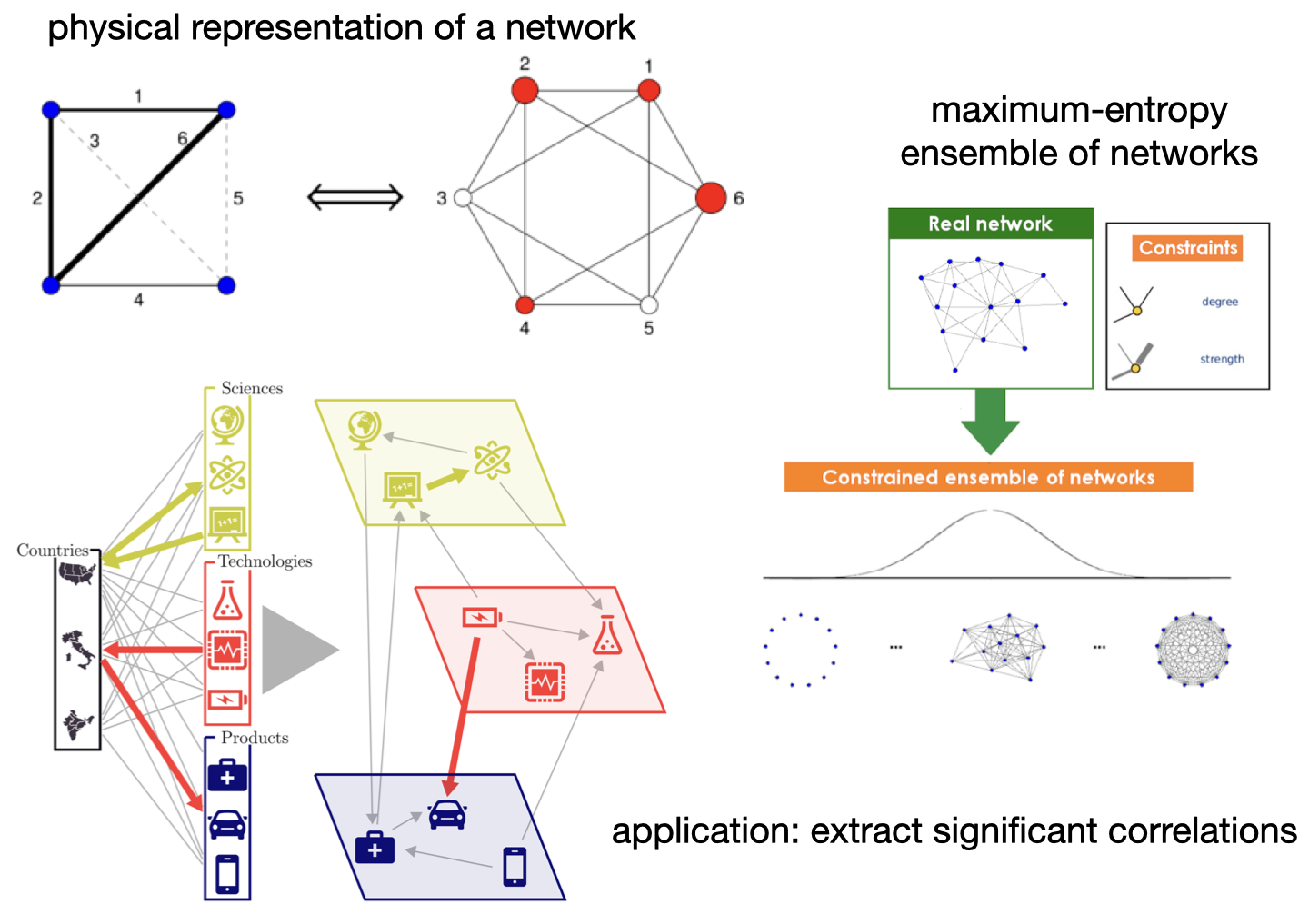
FIG8: Statistical mechanics of networks and applications
The research activity pertains the study of out-of-equilbrium statistical mechanics, dynamical systems and complex fluids across scales: from small scales (kinetic theory, population dynamics, micro- & nanofluidics) to large scales (dynamics of turbulent flows), focusing on fundamental studies in the context of fluid dynamics, but also on more general aspects (statistical mechanics of networks and their applications). Theoretical and mathematical tools are involved, as well as high performance computing.
Staff Members (with link to the publications):
Turbulent flows: Understanding the behavior of turbulent flows’ dynamics is one of the most intriguing, frustrating and important problems of classical physics (FIG1). It is a fact that in many cases fluids have complex dynamics with a dominant role in determining the physics of the system, regardless of the scale at which the flow occurs. Despite the central role that turbulent fluids play in the universe, their dynamics remains in many ways indecipherable. It is almost trivial to remember turbulence as the last unsolved problem of classical physics. In reality, turbulence is much more than a single problem, it is a vast field of study with central applications in engineering, geophysics, astrophysics up to pure mathematics. It is from the effort that physicists have devoted during the last decades to the study of turbulence, that various ideas and tools later used in different areas of physics have been developed. An example is the concept of anomalous diffusion (which has recently become popular during the Covid19 pandemic due to its importance in determining the propagation of viral molecules in the surrounding environment!) or the powerlaw scaling used to study many-body problems. Important notions such as scale invariance and universality were first proposed in the context of turbulence. The main difficulties in this field come from the fact that we are dealing with an out of equilibrium system with a dynamics depending on many degrees of freedom strongly coupled and capable of developing extreme fluctuations in the velocity field. The research group at the Physics Department in Tor Vergata has been studying for several years the behavior of complex fluids with both a theoretical and numerical approach, the latter thanks to the use of supercomputers either from the European computer centers or in-house.
More recently, part of the research activities have focused on the applications of Artificial
Intelligence techniques such as Machine Learning (ML) and Reinforcement Learning (RL) to the study of complex fluids and flows. Some of the most prestigious results have allowed us to understand how to use Eulerian probes (fixed in space) or Lagrangian (which are transported by the flow) to optimize and control some properties of the fluid, including the presence of extreme events in the dissipation and enstrophy fields (FIG2). Similarly, new big-data and ML techniques are being developed to improve the data assimilation algorithms, necessary in the field of numerical meteorology to develop new and more accurate forecasts also at a climatological level for global warming.
Staff members involved:
Prof. Luca Biferale, Dr. Michele Buzzicotti, Dr. Fabio Guglietta, Prof. Roberto Benzi
Kinetic theory (theory and simulations): kinetic theory, in the modern sense of the term, indicates the study of physical problems that can be described by appropriate equations for distribution functions, which give an effective description of the dynamics of a system consisting of a large number of interacting elements. The prototype is the Boltzmann equation, which describes the state of a gas out of equilibrium and has shown for the first time the connection with hydrodynamical equations of motion at larger scales. Fundamental issues in non-equilibrium statistical mechanics are the derivation of the Boltzmann equation from Newton's equations and the derivation of hydrodynamic equations from the Boltzmann equation. From the mathematical point of view, the open problems pertain the existence of solutions for the Boltzmann equation, especially in stationary situations and in presence of generic geometries. Kinetic theory has also a wider field of application, ranging from traffic models, to models for granular media, models that describe the motion of birds (fish etc), colloidal particles, population evolution models and many others.
Especially in recent years, new computational models, known as 'Lattice Boltzmann Models'
(LBM) have been developed from suitable space-time discretizations of the Boltzmann equation. The Tor Vergata research group has made important contributions to the development of LBM, with fields of application traditionally oriented towards the understanding of the phenomenon of fully developed turbulence. More recently, there have been also developments towards the numerical simulation of complex fluids at small scales (micro- and nanofluidic, FIG3,FIG4) and in the presence of complexities such as thermal fluctuations, multiple phases/components (systems with complex rheology), membranes and nonideal interfaces (FIG5).
Staff members involved:
Prof. Rossana Marra, Prof. Mauro Sbragaglia, Dr. Fabio Guglietta, Prof. Roberto Benzi
Population dynamics: Population dynamics (PD) is a long-standing research field in biology, mathematical physics and statistical mechanics. Many qualitative and quantitative features of micro-organisms spreading, observed in natural environments as well as in laboratory, are successfully understood. In realistic settings, for population living in fluid environment, it is largely unknown, both theoretically and experimentally, how the phenomenology of PD is changed by the presence of turbulence. In particular, if turbulence is even weakly compressible, a new and rich phenomenology occurs and many new features appear in the system. Small compressibility (due, for instance, to the buoyancy in stratified flows, inertial effects, gyrotaxis, …) is responsible for clustering of biological entities (FIG6, FIG7). Clustering also implies reduction of the biological mass and enhancement of the effects associated to number fluctuations. The research focuses on the enhancement or inhibition of selective advantage in PD subject to advection of turbulence .
Staff members involved:
Statistical mechanics of networks and applications: Complex networks are systems described by a nontrivial pattern of interactions between their constituent units, which typically leads to emergent properties such as scale invariance, small-world-ness and hierarchical/modular structure (FIG8). The physics of networks can be derived by treating the connections themselves as the particles of the system. In particular, statistical mechanics models are derived from the principle of maximum entropy by constraining local and heterogeneous network features. These models can be used in practice to make unbiased inference about the network in case of incomplete knowledge, or to detect significant deviations that may reveal important information on the system.
Staff members involved: